There are many, many things you can configure in your high-end fitness tracker / smart watch. Not all of them are well documented, so although you can usually find out what a certain feature does, there may not be enough information to help you decide if and when you should be using it. Or if it even works – don’t get me started on automatic lactate threshold / VO2 max / performance condition readings when all your runs are over hilly ground.
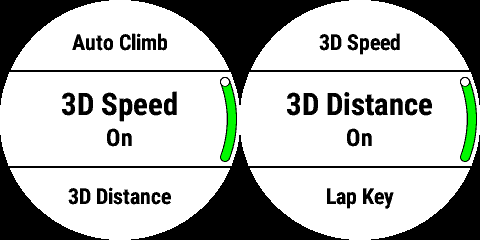
I digress. One feature of much questioned value is the inclusion of 3D data when working out your speed and distance during activities. From Garmin’s own support pages:
The 3D Speed and Distance features change the way compatible outdoor wearable devices* read speed and distance.
3D Speed – Calculates speed using both the elevation change and horizontal movement over ground.
3D Distance – Calculates the distance traveled using both elevation change and horizontal movement over ground.
When you think about it, this should be a no-brainer; a 10k run with 1000m of elevation changes isn’t a 10k run along a beach, so why not take into account that lovely hilly data? On the Fenix 5 series at least, Garmin has addressed that conundrum by giving you the option of including 3D data. Which I’ve always found a little odd, almost as if you’re being given the option of beta-testing something that may or may not work, i.e. if it works properly then why isn’t it baked into all activities? So I did a little test.
An Experiment
The aim was to find out what impact (if any) was achieved by switching on both 3D Speed and 3D Distance settings. I’d do this by going for a sufficiently long, reasonably hilly run, and then immediately repeating the same route, albeit in reverse. On the outward leg the 3D settings would be off, on the homeward leg I’d switch them on. I tried to find a course with roughly equal amounts of elevation gain and loss so that there wouldn’t be too much variance between the two test candidates, and ran them both back-to-back to minimise the impact of barometric changes affecting altitude readings.
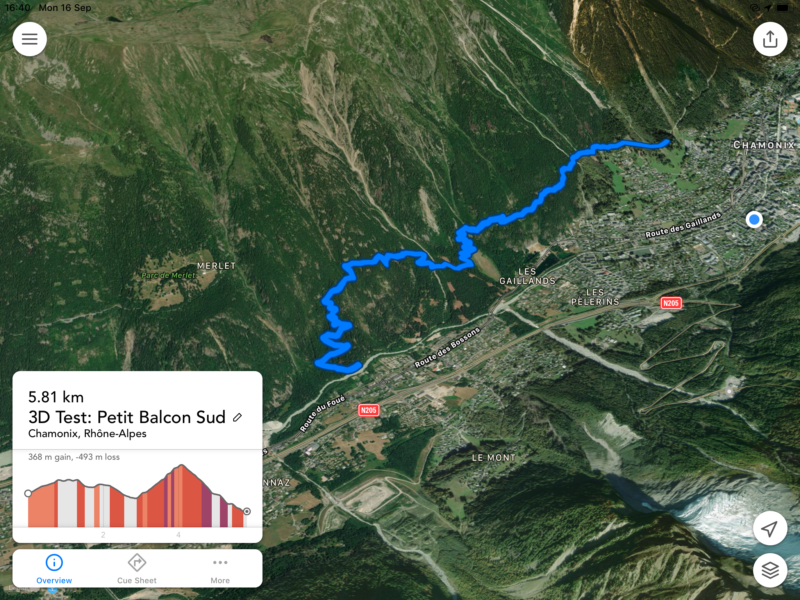
I chose a section of the Petit Balcon Sud in Chamonix because it offered some gentle climbs and descents which would keep me moving and provide some good 3D data. And because I’m staying in alps right now, where it’s either flat or extremely hilly, with little in-between. I’d set off from the Pierre à Ruskin (just behind the Brevent cable car) and head south-east along the northern edge of the valley until reaching Les Montquarts just under 6km later. Here’s how that went on the outward leg:
My Fenix 5 tells me I covered 5.68km in 1:00:49 at an average pace of 10:42 min/km. I gained 345m and lost 484m of elevation along the route, and burned 583 calories, bringing with it a training effect of 3.3 aerobic / 1.4 anaerobic.
Some Predictions
What was I expecting to see on the return leg? Nice though it would be, I didn’t rate my chances of completing the second activity in exactly the same time as the first, given changes in temperature, the amount of water I was left carrying, occasional photo stops, etc. So 3D Speed analysis might have to be shelved, but 3D Distance should be interesting, right? I’d made sure to start / stop the activities in exactly the same location, and GPS+GALILEO should give me a consistent signal despite light / occasional tree cover. As per the first activity I wore Garmin’s own premium chest strap (since optical HR is worse than useless) and had my Fenix 5+ paired with a Foot Pod and Tempe.
Back to the question, what was I expecting to see? It’s easy to measure the distance covered by a runner moving from point A to point B along a flat plane, even if there are many twists and turns. But what if there are also lots of small changes in elevation between point A and point B? An easy answer would be to reach for Pythagoras Theorem, and speculate that the actual 3D distance covered is equal to the hypotenuse, with the non-3D distance being the horizontal component of the triangle and the elevation difference being the vertical component.
I know I covered 5680m horizontally, and am going to suggest that the vertical component should be the sum of gain and loss instead of the net difference between start and finish, otherwise a mountain marathon would have zero 3D impact as long as it starts and ends in the same place. In my case that’s 345m + 484m = 829m of elevation difference. Using Pythagoras I predict a 3d Distance of 5.74 km:
56802 + 8292 = 57402
But is Pythagoras a valid way to work out 3D Distance? I doubt it, since I wasn’t moving along a smooth incline between start and finish. A real world elevation profile would look more like the teeth of a saw, and is likely to be much longer than our theoretical hypotenuse when stretched out. To work this out accurately you’d probably have to apply Pythagoras to each individual change in elevation and then combine them at the end. But that’s too much work, so I’m going to say that I expected at least 5.74km with 3D distance enabled.
And the Winner is …
With 3D Distance and 3D Speed enabled, I measured the return trip at 5.59km, some 90m shorter than the first attempt, which could easily have been due to GPS signal fluctuations over that kind of distance and terrain. It took me 5 minutes longer but interestingly I did burn 66 more calories, probably through unintentional interval work as I picked up the pace following a series of photo stops. Training effect was down to 3.1 aerobic but up to 2.3 anaerobic.
I think it’s safe to say that 3D Speed and Distance don’t produce any tangible effect under what I’d call typical conditions, and will henceforth remain switched off.





I’d like to point that your set-up was flawed in many instances. If you were to repeat the test, please consider the following:
1- If you were using a footpod and either speed or distance (or both) we’re set to come from the footpod the whole experiment is over. 3D speed is only supposed to work if speed is coming from GPS. The watch will NEVER combine information from two sources. It either displays spped from the footpod (and in this case the 3D option will be ignored even if you selected ON) or display the speed derived from different GOS coordinates and in that case alone the 3D speed could make a difference.
2- Same goes for 3D distance.
3- Although in the real world going and then coming back the same path would result in the same distance, that is not true in result you’ll get from the GPS. Watch position changing will probably interfere in the way your body and your surroundings affects how straight or how dirt (by colliding with the environment) the signal will be. The best way to do it is to go one day with page and speed from GPS with 3D speed and distance off and then go another day, the very same path, now with 3D speed and distance on.
Think about doing it in case it’s a route you run repeatedly anyway.
Good luck!
Thanks for the feedback, I appreciate it!
With regards to points 1 & 2, Garmin’s Foot Pod support pages state: “The source for pace/speed while running outside comes from GPS” so I don’t see how wearing the Foot Pod for the test invalidates it. My understanding is that the Foot Pod kicks in when GPS signal is patchy (e.g. under heavy tree cover) or when there’s no signal at all, like when you’re running indoors. At all other times I would expect the Foot Pod to be periodically calibrated so that it’s accurate when needed.
Having said that, I can imagine that using a distance measuring device (Foot Pod, wheel sensor, etc) would override 3D speed / distance since it’s already measuring the real distance between two points – the hypotenuse, in my example – and has no need for adjustment via elevation data. I found a similar discussion over on Garmin Forums but without an explanation from the manufacturer or empirical test data its no more valid that my experiment or your theory. If you can share a link to a more detailed explanation from Garmin I’d appreciate it, because everything I’ve seen from the manufacturer is pretty vague.
With regard to your third point, I don’t understand how direction has any impact at all on the overall distance between two points as measured by GPS. The tree cover is the same, the mountains are the same, just in reverse. In an ideal world I would do the test in the same direction both times, but not on different days, since mountain weather is changeable and part of the experiment relies on barometric pressure.
Unfortunately I don’t have the opportunity to repeat the same route right now, but I can find a hilly course closer to home, and don’t mind running two circular loops on the same day. As long as it’s not more than 10 km. I’m not that fit. How much elevation gain should I aim for on a 5 km course in order to test 3D ‘on’ versus ‘off’?
Thanks again!